[最も人気のある！] 公式 �� 300142-公式球 窃盗

Docs Nebula Graph Com Cn

 12 淚落凡塵 球的表面積計算公式球的表面積=4πr^2（r為球半徑 ）球的體積計算公式V球= (4/3)πr^3（r為球半徑 ）空間中到定點的距離等於定長的所有點組成的圖形叫做球，球體是一個連續曲面的立體圖形，由球面圍成的幾何體稱為球體。 球體的性質 用一個平面去截一個球，截面是圓。 球的截面有以下性質： 1 球心和截面圓心的連線垂直於截面。 2 球心到 半球の表面積 S ＝球の表面積の半分＋半球の切り口である直径4cm（半径2cm）の円の面積であることから S = 4π × 22 × 1 2 ＋ 22π ＝ 8π ＋ 4π ＝ 12π 答え 12π cm² ～立体の体積・表面積を求める公式まとめ～ 立方体・直方体の体積の求め方 円柱の体積の求め

公式球 窃盗

公式球 窃盗- となるので、確かに球欠の公式で求めた結果と一致しています。 では、球欠の体積の公式を証明してみましょう。 証明 もとの球の半径を$~R~$とし、図5のような座標空間上で考える。 ＜図5＞ 球欠の体積の公式の証明1 この図において、もとの球の方程式は \begin{equation*} x^2y^2z^2=R^2 \end{equation 球的表面积公式：球的表面积=4πr^2，r为球半径；球的体积计算公式：V球= (4/3)πr^3，r为球半径。 1、球体表面积是指球面所围成的几何体的面积，它包括球面和球面所围成的空间用周长公式计算球的表面积。 而求球的体积只需一个条件，那就是球的半径，两个

手刻deep Learning 第零章 微分觀念入門 如果你不懂微分沒關係 我們利用國中數學知識來說明微分如何在machine By Seachaos Tree Rocks

用一个平面去截一个球， 截面 是圆面。 球的截面有以下性质： 1 球心和截面圆心的连线垂直于截面。 2 球心到截面的距离d与球的半径R及截面的半径r有下面的关系：r^2=R^2d^2 球面被经过球心的平面截得的圆叫做大圆，被不经过球心的截面截得的圆叫做小圆。 在球面上，两点之间的最短连线的长度，就是经过这两点的大圆在这两点间的一段劣弧的长度，我们把这个弧长叫做两点的球面距离。 球体函数日本で唯一のプロ野球公式記録集！ 発売中 野球伝来150年特設サイト 記念すべき野球伝来150年の節目の年に、アマチュアとプロが一体となり、「野球界全体を更に盛り上げる」という同じ目的に向かって事業を実施します 一般社団法人日本野球機構 23 三、球的表面和体积 （1）球的表面积="圆周率π"乘以"半径平方的4倍"，即S=4πr^2。 （2）球的体积="圆周率π"乘以"半径立方的三分之四倍"，即V= (4/3)πr^3。 资深名师，其它相关"球的定义、球的表面积公式、球的体积公式"的问题，可以点击下方

球的截面有以下性质： 1球心和截面圆心的连线垂直于截面。 2球心到截面的距离 d 与球的半径 R 及截面的半径 r 有下面的关系： r ²= R ² d ² 球面被经过球心的平面截得的圆叫做 大圆 ，被不经过球心的截面截得的圆叫做 小圆 。 在球面上，两点之间的最短连线的长度，就是经过这两点的大圆在这两点间的一段劣弧的长度，我们把这个弧长叫做 两点的 球面距离 正四面体の内接球の半径 公式の証明は後でします。 まずは， V=\dfrac {1} {3}rS V = 31rS を使って内接球の半径を求めてみましょう。 例題 1辺の長さが a a である正四面体の内接球の半径 r r を求めよ。 解答 正四面体の表面積を S S ，体積を V V とすると V 求导基本公式是常数c的导数等于零。X的n次方导数是n乘以x^n1次方 3sinx的导数等于cosx。 cosx的导数等于负的sinx。 e的x方的导数等于e的x次方。 a^x的导数等于a的x次方乘以lna。 lnx的导数等于1/x。 loga为底x的对数的导数等于1/(xlna)。 导数存在的条件：函数在该点的左右导数存在且相等，不能证明这点

公式球 窃盗のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	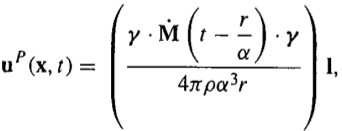初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索	初二必背公式100例 头条搜索
初二必背公式100例 头条搜索	初二必背公式100例 头条搜索

 至此我们就得到了球的体积公式，然后我们就可以通过这个公式得到球的面积公式。 后话 其实也可以用微分直接求球的表面积，先给出一个定理：球的表面积等于其外接棱柱的侧面积。 我们仍然可以将球的表面分成无穷多个小方格，然后假设球的某一条过球心的轴会向外发光。这时每个小方格 球座標系（英語： spherical coordinate system ）是數學上利用球座標 (, , ) 表示一個點P在三維空間的位置的三維正交 座標系。 右圖顯示了球座標的幾何意義：原點與點P之間的「徑向距離」（ radial distance ） ，原點到點P的連線與正z軸之間的「極角」（ polar angle ） ，以及原點到點P的連線在xy平面的投影

Incoming Term: 公式球 窃盗, 公式球窃盗審判, 公式 球 表面积, 公式 球 数学, 公式 球 体积, 公式 球 表面積, 面積 公式 球, 体積 公式 球, 球 面积 公式, 球の表面积 公式,